Earlier today I set the following two puzzles. Here they are again with solutions.
The first is by Randall Munroe, cartoonist of the webcomic xkcd and author of the bestselling book What If?
1. All Together Now
Find all the possible ways, if any exist, to fill in the three blanks to make all three statements true.
Solution There are three ways, some more interesting than others!
Let the blanks be represented by x, y and z.
If we are only considering the numbers in the blanks – there is only one solution x = y = z = o. The ‘joke’ is to realise that we can include the numbers of the panels. In this case, there are two solutions.
The panels become three equations: x = 5 + y + z, y = √3xz, and z = min (x, y, 1)
Let’s say min (x, y, 1) = y. So z = y, thus x = 2y + 5, and y = √3xy. This simplifies to y2 + 3y = 0. We know y is bigger than or equal to 0, since it is the value of a square root, so y= o. Giving us one solution: x = 5, y = z = o
Now let’s say min (x, y, 1) = x. Thus z = x, and y = –5, which is a contradiction since y is bigger or equal to 0.
When min (x, y, 1) = 1, we get the second solution: x = 12, y = 6, z = 1.
2. One to Venn
The four squares below form a Venn diagram with ten regions, labelled A to J. The letters A to J each stand for a number between 1 and 10, such that no two regions share the same number and all numbers from 1 to 10 are used. The regions in each square add up to the same number. What value is D, the intersection of all four squares?
Solution: D = 7
Since the sum of the regions is the same for each square, when two squares intersect, the regions that do not intersect must be equal. So, for the red and green squares, illustrated below, A = G + H + I.
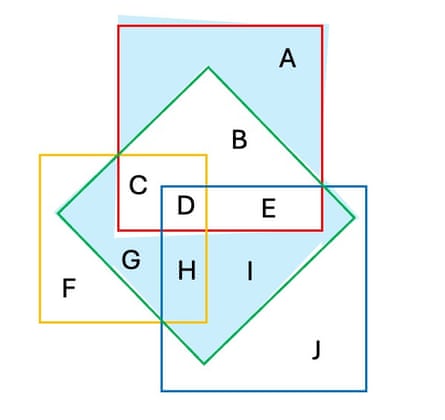
Likewise, F = B + E + I, and J = B + C + G.
Thus A+F+J = G+H+I+B+E+I+B+C+G
= 2(G+I+B) +C+E+H.
The highest possible value of A+F+G is 10 + 9 + 8 = 27.
The lowest possible value of 2(G+I+B) +C+E+H is 2(1 + 2 + 3) + 4 + 5 + 6, which is also 27.
It follows that both of these values are 27. The only number missing is 7, and the only missing label is D, so D = 7.
I hope you enjoyed today’s puzzles. I’ll be back in two weeks.
Both of today’s puzzles are taken from The Mathematical Playground: People and Problems from 31 Years of Math Horizons. Math Horizons is the undergraduate magazine of the Mathematical Association of America, and the book, a compilation of its best puzzles, is full of great material. For more information see here.
What If? (10th anniversary edition) by Randall Munroe will be out in the UK on November 14.
My latest book is Think Twice: Solve the Simple Puzzles (Almost) Everyone Gets Wrong. (In the US it is called Puzzle Me Twice, and out tomorrow.) To support the Guardian and Observer, order your copy at guardianbookshop.com. Delivery charges may apply.
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.




